1.1 Real Numbers
- Cecilie
- 12. aug. 2016
- 3 min læsning
1.1.1 The Number Line
⭐️ ℕ = Natural numbers
⭐️ ℚ = Rational numbers
⭐️ ℝ = Real numbers
⭐️ ℤ = Integers
We can illustrate the real numbers, ℝ, by making an infinitely long number line. Each number on the axis represents one real number:

The real numbers include
The natural numbers, ℕ:
ℕ = {1, 2, 3,...}
Integers, ℤ:
ℤ = {..., -3, -2, -1, 0, 1, 2, 3,...}
The rational numbers, ℚ:
Simple fractions, e.g. 11/8, 1/2, -18/5 etc.
The irrational numbers
Numbers that cannot be written as a simple fraction, e.g.: √2 and π
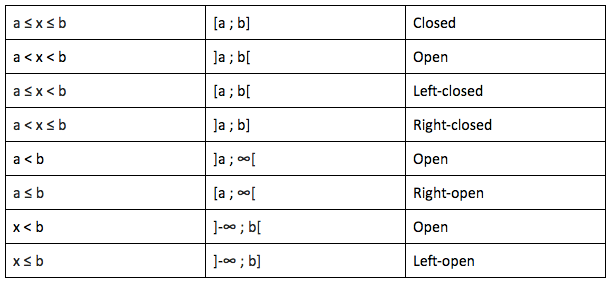
1.1.2 Intervals
⭐️ Closed interval: Interval that includes its endpoint.
⭐️ Open interval: Does not include its endpoints.
⭐️ ℝ = Real numbers = ]-∞ ; ∞[
We often work with only a selected part of the real numbers, ℝ, e.g.:

The amount of numbers corresponding to the line segment is written like this:
[-1 ; 5]
This is what we call a closed interval: From -1 up to 5 including both numbers.
This interval corresponds to the real numbers that meet:
-1 ≤ x ≤ 5
When the brackets turn away from the number the number is not included in the interval:

The interval [-2 ; 7[ includes all real numbers between -2 and 7, where -2 is included but not 7.
In other words, all numbers, x, that meet:
-2 ≤ x < 7
Take a look at:

On the number line the numbers are maximum 2, but has no lower limit – in other words the numbers, x, that satisfy:
x ≤ 2
We show that there is no lower limit by using the symbol: - ∞. The brackets have to turn away from ∞ and -∞. This interval is thus written like this:
]- ∞ ; 2]
Furthermore, we can have an interval ]-4 ; ∞[ which are the numbers, x, that satisfy
]-4 ; ∞[
This is what we call and open interval.
This leaves us with:
ℝ = ]-∞ ; ∞[
Table 1: Types of intervals
1.1.3 Intersections and unions
⭐️ ∈ = ... is an element of...
⭐️ ∉ = ... is not an element of...
⭐️ ∅ = no elements.
⭐️ ∩ = intersected with...
⭐️ ∪ = union
Intersection
-2 is a number in [-6 ; 4[ which we denote:
-2 ∈ [-6 ; 4[
This means that -2 is an element of (∈) [-6 ; 4[.
10 is not in the interval ]12 ; 15[ which we denote:
10 ∉ ]12 ; 15[
With this denotation:
x ∉ [a ; b] when a≤ x ≤b
We have a statement:
1≤ x ≤5 and x<2 (*)
1≤ x ≤5 means that x is in the interval [1 ; 5]
x<2 means that x is in the interval ]- ∞ ; 2[
→ (*) is equivalent to: x lies in both intervals.
→
For all values of x that are in both intervals are equivalent to:
[1 ; 2[
This last interval is what we call an intersection. It is denoted:
[1 ; 5] ∩ ]- ∞ ; 2 [ = [1 ; 2[
The intersection is thus the numbers that both intervals have in common.
If an intersection is one or more individual numbers we denote: { }
If there is no intersection is empty – this is denoted: ∅
Example 1:
[3 ; 6] ∩ [4 ; 7[ = [4 ; 6[
Example 2:
[5 ; 2] ∩ ]2 ; 4[ = Ø
[0 ; 3] ∩ [3 ; 12] = {3}
Union
-2 ≤ x ≤ 6 or x<1 (*)
This means that x has to be in either [-2 ; 6] or in ]1 ; ∞[
In other words: x has to be in one of these two intervals but can be in both.
→
x has to be in [-2 ; ∞[. This is the interval that is called the union. We denote it like this:
[-2 ; 6] ∪ ]1 ; ∞[ = [-2 ; ∞[
The union of two intervals can never be empty (Ø)
Sometimes the union and the intersection is one and the same thing, but this is not always the case.
Example 3:
]- ∞ ; 5] ∪ ]-1 ; ∞[ = ℝ
(In this example the intersection would be ]-1 ; 5]

Kommentarer